[LeetCode] TIL LeetCode: 448, 977(review)

448. Find All Numbers Disappeared in an Array

Problem type - Array

🧩 Problem

🎯 Strategy

Understand the concept

The concept is pretty straightforward, in which we have to return missing integers, where the array nums of n integers are in the range [1, n].

Regular approach

for-loop approach

The normal approach to this problem would be the for-loop approach, but we need to use the function abs() to achieve the goal.

The main algorithm is as we loop through the array, we will set a temporary variable a and set it as abs(num) - 1 to track the index. If the nums[a] is negative, we already changed the value so that we will skip the value.

Suppose the array is in increasing order. The output of the algorithm looks like this:

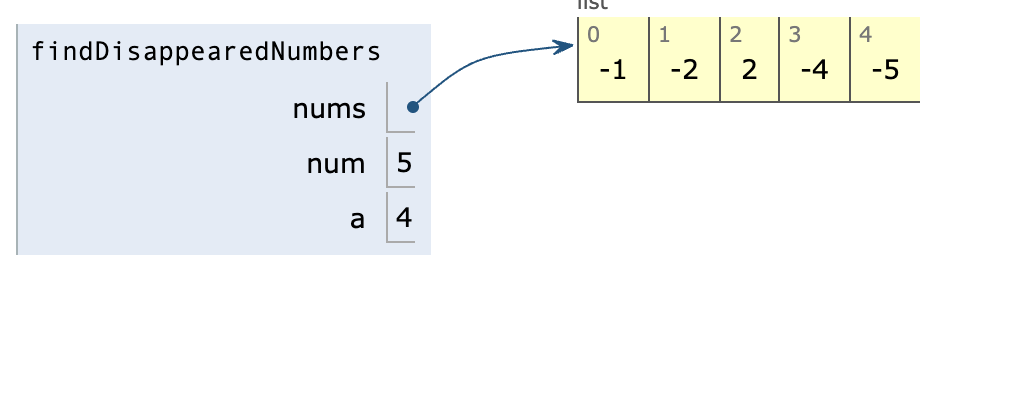
Notice that the duplicated value num[2] is not converted into the negative value. Apparently, we are missing three here.

def findDisappearedNumbers(self, nums: List[int]) -> List[int]:
        for num in nums:
        	a = abs(num) - 1
            if nums[a] > 0:
            	nums[a] *= -1
        ...

We will need an index and the value of that index to return the result array. Hence, we will use the enumerate() function to get both values. The returning array value should be index + 1, since the array starts from zero.

def findDisappearedNumbers(self, nums: List[int]) -> List[int]:
        for num in nums:
        	a = abs(num) - 1
            if nums[a] > 0:
            	nums[a] *= -1

        return [i+1 for i,n in enumerate(nums) if n > 0]

The time complexity is O(n) because the function iterates the array twice, once we derive a new nums array and once to build the result list. Both iterations are linear with respect to the size of the input array.

The space complexity is O(1), as the code uses a constant amount of extra space regardless of the input size.

Pythonic approach

set() approach

In Python, we have a set function to deduct duplicated values. By using this function, we can reduce the above code to two lines.

First, we will make the new array to count all the numbers in the range from one.

def findDisappearedNumbers(self, nums: List[int]) -> List[int]:
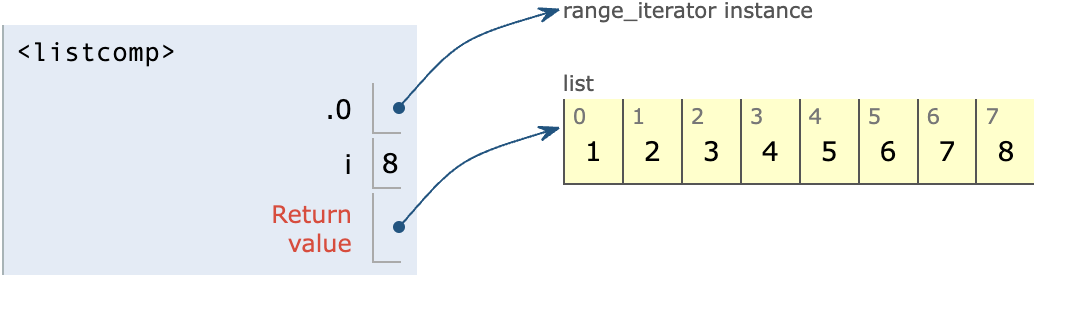
        list_a = [i for i in range(1, len(nums) + 1)]

For instance, in example 1, the list_a will be like this:

Then, we use the set() function to deduct any duplicated value from the list_a, as well as the array nums.

The problem is that we want the missing numbers from the array, and we can simply subtract the nums array from the list_a.

Lastly, we will return the results in the array with the list() function.

def findDisappearedNumbers(self, nums: List[int]) -> List[int]:
        list_a = [i for i in range(1, len(nums) + 1)]

        return list(set(list_a) - set(nums))

The time complexity is O(n) because building the list_a takes O(n) times since it iterates through the range from one to the length of nums. The .set() operation also takes O(n) time.

The space complexity is O(n) where n is the length of the input array nums. The list_a creates a new array, and the .set() operations create two additional sets.

One-liner approach

With the above approach, we can think of the one-liner approach to condense two lines into a single line.

We can achieve this goal by merging the first and second lines.

def findDisappearedNumbers(self, nums: List[int]) -> List[int]:
        return set(range(1, len(nums) + 1)) - set(nums)

This approach shares the same time and space complexity as we just modified the code above.

📌 Thoughts

I still struggle with modifying the array and the usage of the set() function.

In the next chapter, I will encounter more array-type problems and hope to get familiar with these types and solutions.

💻 Solution

for-loop approach

def findDisappearedNumbers(self, nums: List[int]) -> List[int]:
        r

set() approach / one-liner

def findDisappearedNumbers(self, nums: List[int]) -> List[int]:
        return

🔖 Review

Problem type - Array

This is a review problem, so there is no strategy part. But there will be three approaches: the in-place approach, the one-liner approach, and the two-pointers approach.

🧩 Problem

💻 Solution

In-place approach

def sortedSquares(self, nums: List[int]) -> List[int]:
        for i in range(len(nums)):
        	nums[i] *= nums[i]

        nums.sort()

        return nums

The time complexity is O(nlongn) because the sort() function has a time complexity of O(nlogn). The sorting operation dominates the overall time complexity.

The space complexity is O(1) because the algorithm modifies the input array in place.

One-liner approach

def sortedSquares(self, nums: List[int]) -> List[int]:
        return sorted([i**2 for i in nums])

The time complexity is O(nlogn) because the sorted() functions also has a time complexity of O(nlogn)

The space complexity is O(n) because the list comprehension creates a new list containing the squared values. The size of this list is proportional to the size of nums

Two-pointer approach

def sortedSquares(self, nums: List[int]) -> List[int]:
        n = len(nums)
        result = [0] * n

        left, right = 0, n-1
        i = n-1

        while left <= right:
        	left_sq = nums[left] ** 2
            right_sq = nums[right] ** 2

            if left_sq >= right_sq:
            	result[i] = left_sq
                left += 1
            else:
            	result[i] = right_sq
                right -= 1

            i -= 1

        return result

The time complexity is O(n) because the algorithm uses a two-pointer approach to iterate through the sorted squares in non-decreasing order. The while loop runs in linear time.

The space complexity is O(n) because the algorithm uses an additional array result to store the squared values.

📌 Thoughts

Throughout the course, I’m getting used to the two-pointer approach. But the last solution was ambiguous when I saw the question. I need to practice more and more problems like this question.

The first chapter is over, and the next chapter will be the array and string.