[LeetCode] TIL LeetCode: 88

88. Merge Sorted Array

Problem type - Array

🧩 Problem

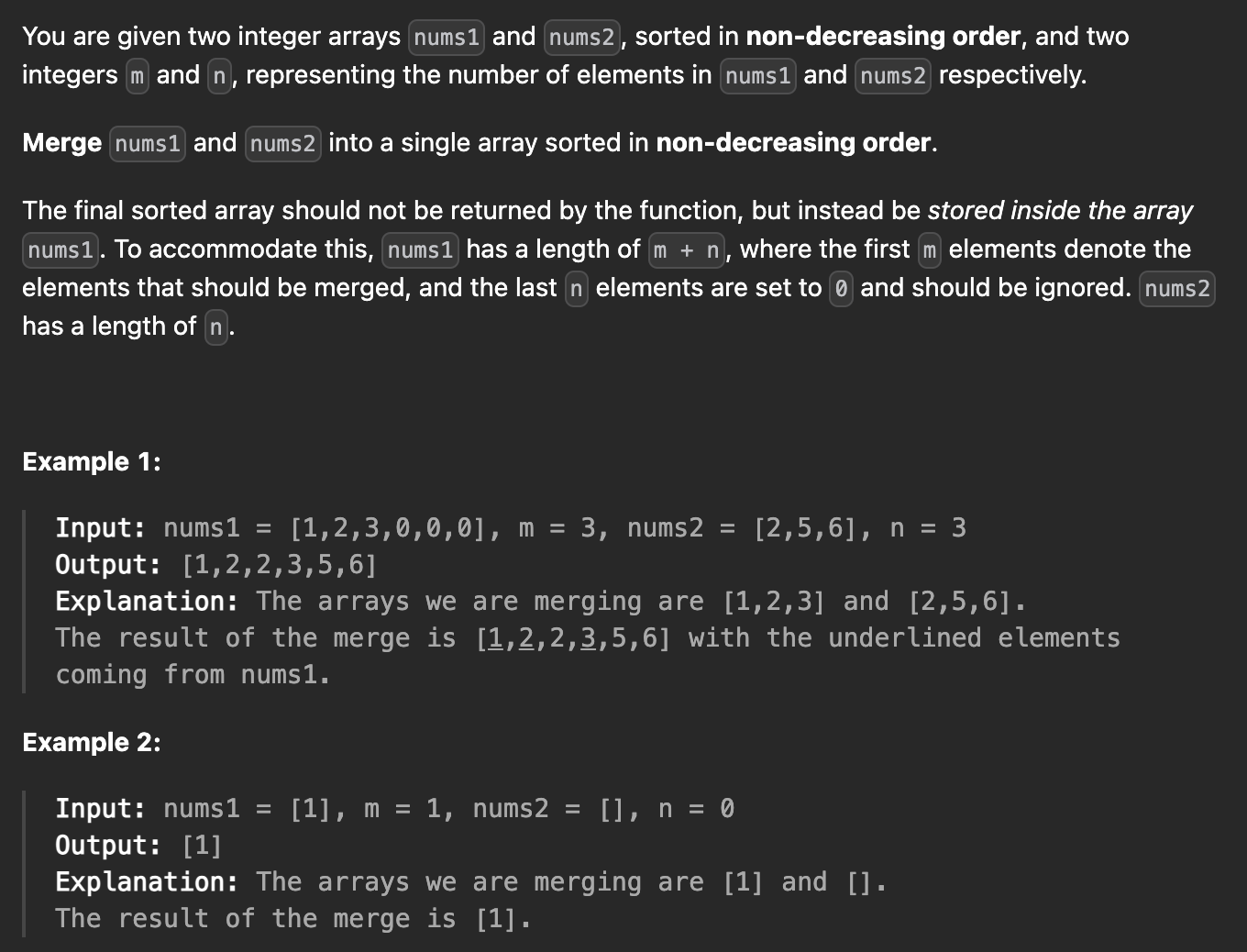
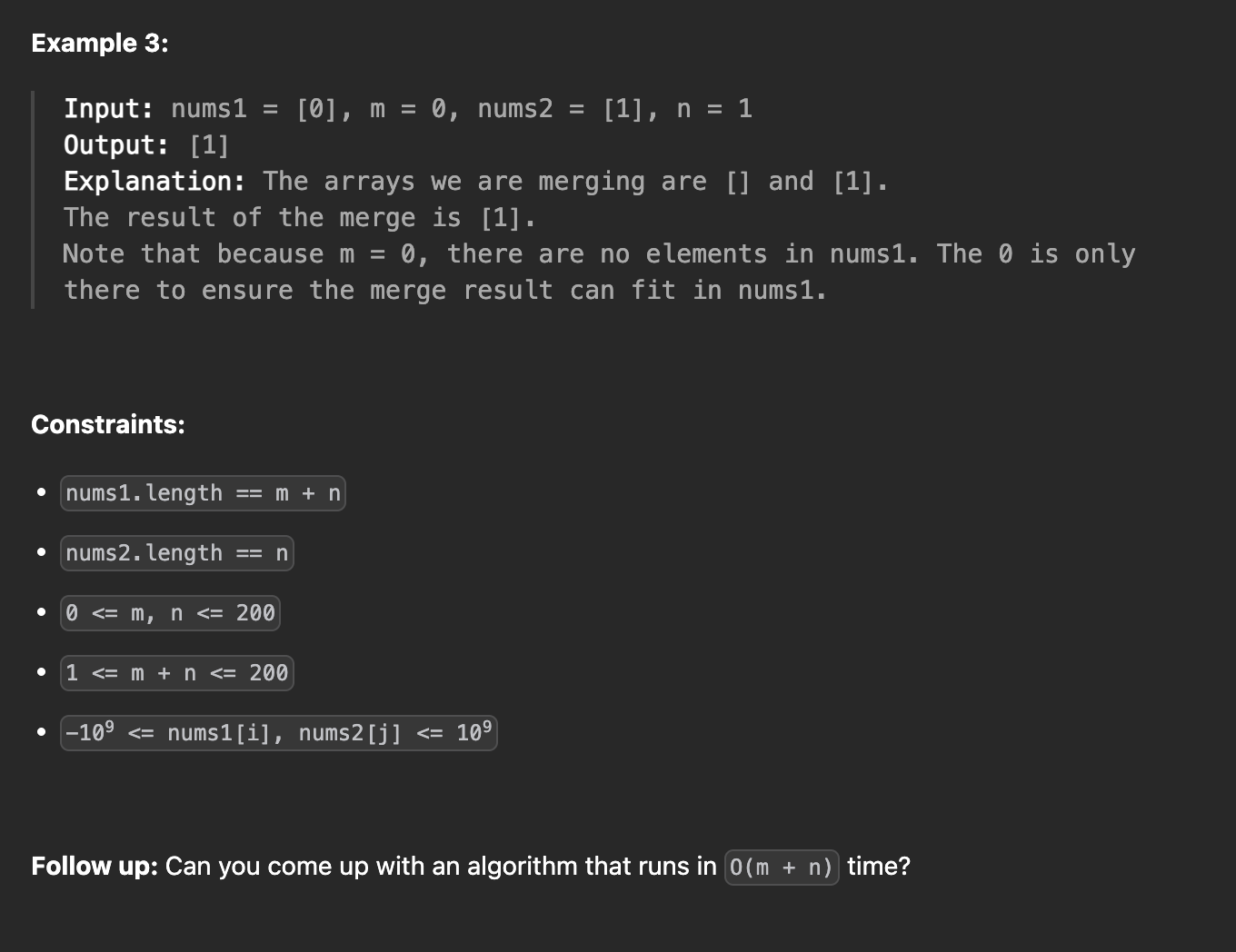
🎯 Strategy

Understand the concept

There are so many ways to solve this problem, and I will go over from the very beginning to a little more complex approach.

The basic concept is we are merging two arrays, and the first solution that came up was adding two arrays together and sorting the final array.

Is this the best approach? We will find out with the following steps.

Looping approach

Indexing approach

To loop the array, we need to set the range of the loop. In the first case, we will decide to loop as the length of nums1.

Then, replace the 0 with the nums2 values by adding a conditional statement.

def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
        """
        Do not return anything, modify nums1 in-place instead.
        """
        for i in range(len(nums1):
        	if nums1[i] == 0:
            	nums1[i] = nums2[?]

But there is a problem: how should we track the second array’s index?

We can add another variable like j for another index to solve this issue.

def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
        """
        Do not return anything, modify nums1 in-place instead.
        """
        j = 0
        for i in range(len(nums1):
        	if nums1[i] == 0:
            	nums1[i] = nums2[j]
                j += 1

To finish the loop, we have to add one more condition because if we leave it as it is, it is an infinite loop. We can do so by adding if j >= n: break.

At the end, sort the array with .sort() to match it with the provided result.

Here is the final code:

def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
        """
        Do not return anything, modify nums1 in-place instead.
        """
        j = 0
        for i in range(len(nums1):
        	if j >= n:
            	break
        	if nums1[i] == 0:
            	nums1[i] = nums2[j]
                j += 1

        nums1.sort()

The time complexity is O(nlogn), because the .sort() operation typically has an average time complexity of O(nlogn).

The space complexity is O(1), since it doesn’t create any additional data structures or use extra memory. The code only uses a few integer variables.

The loop approach - 2

Although it does the job, it is quite not satisfying. The n could have 0, which might cause the issue.

This time, we are going to create a loop that has a specific range. Since the m and n represent the integer, we can use it as a reference.

def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
        """
        Do not return anything, modify nums1 in-place instead.
        """
        for i in range(m, m + n):

Since the nums1 == [1,2,3,0,0,0], we should add nums2 values where the positions of 0s.

Then, we should merge two arrays with some conditions. In case 1, the loop index i starts at m == 3 and end at m+n == 6.

def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
        """
        Do not return anything, modify nums1 in-place instead.
        """
        for i in range(m, m + n):
        	nums1[i] = nums2[i - m]

Hence, we can use i-m == 0 to get the first value of the nums2 array. The loop will stop when it reaches the end of the range.

Sort the array to match the style of the result. The final code snippet will look like this:

def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
        """
        Do not return anything, modify nums1 in-place instead.
        """
        for i in range(m, m + n):
        	nums1[i] = nums2[i - m]

        nums1.sort()

The time complexity is O(nlogn) because the sort operation takes O(nlogn), the dominant factor.

The space complexity is O(1) because the code operates in-place, modifying the nums1 array without creating new arrays.

Advanced Approach

Slicing approach

We can use the same idea as the above, but this time, we will use the slicing technique.

If the m is the count without 0, we can slice it and merge two arrays.

We can condense several lines of code in one line.

def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
        """
        Do not return anything, modify nums1 in-place instead.
        """
        nums1[:] = sorted(nums1[:m] + nums2)

Where [:] means the whole array, [:m] means slice the array from the start to nums1[m-1].

The time complexity is O(nlogn). The space complexity is O(n) because the code creates a new list by concatenating nums1[:m] + nums2 arrays.

Two pointers approach

Lastly, we will solve this question in the two pointers approach.

Create p1; this will be the index of nums1 numbers except for 0s. In the same manner, create p2 to represent the index of the nums2 array.

Finally, create another variable for the last index of the original nums1 array.

def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
        """
        Do not return anything, modify nums1 in-place instead.
        """
        p1 = m - 1
        p2 = n - 1
        k = m + n - 1

The algorithm process will be like this:

1. There are three reference, nums1[p1], nums2[p2], and nums1[k]. The pointer p1, p2 checks the value and conditionally replaces values in nums1 with the index k.
2. We are going to check nums[p2] values with nums1 array from the end.
3. Compare the value of nums1[p1] and nums2[p2].
4. If nums1[p1] > nums2[p2], replace the current nums1 array’s last value nums1[k] with nums1[p1] value.
5. If the checking process is over, decrease p1 by one to check the next value. To avoid error, add the p1>=0 condition in the if statement.
6. Else nums1[p1] is not bigger than nums2[p2], the current value nums1[k] = nums2[p2].
7. If the checking process is over, decrease p2 by one.
8. When each step is over, decrease k by one to compare the value in the array.

And this is how we can represent the above in code:

def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
        """
        Do not return anything, modify nums1 in-place instead.
        """
        p1 = m - 1
        p2 = n - 1
        k = m + n - 1

        while p2 >= 0:
        	if p1 >= 0 and nums1[p1] > nums2[p2]:
            	nums1[k] = nums1[p1]
                p1 -= 1
            else:
            	nums1[k] = nums2[p2]
                p2 -= 1
            k -= 1

This is an in-place approach, and it could also be a greedy approach since the nums1 array has to be sorted.

The time complexity is O(n), because the while loop runs for n iterations.

The space complexity is O(1) because it modifies the nums1 array in-place without creating the additional array.

📌 Thoughts

The first two approaches were my initial answer, and I could understand the slicing. Probably, next time, when facing a similar question, I could use a slicing approach.

On the other hand, the two pointers approach is still the way I have to improve. It took quite a while to understand the question, so I should face and practice the same type of questions.

💻 Solution

Indexing approach

def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
        """
        Do not return anything, modify nums1 in-place instead.
        """
        j = 0

        for i in range(len(nums1)):
        	if j >= n:
            	break
        	if nums1[i] == 0:
            	nums1[i] = nums2[j]
                j += 1
        nums1.sort()

Basic loop approach

def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
        """
        Do not return anything, modify nums1 in-place instead.
        """
        for i in range(m, m+n):
        	nums1[i] = nums2[i-m]
        nums1.sort()

Slicing approach

def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
        """
        Do not return anything, modify nums1 in-place instead.
        """
        nums1[:] = sorted(nums1[:m] + nums2)

Two pointers approach

def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
        """
        Do not return anything, modify nums1 in-place instead.
        """
        p1 = m - 1
        p2 = n - 1
        k = m + n - 1

        while p2 >= 0:
        	if p1 >= 0 and nums1[p1] > nums2[p2]:
            	nums1[k] = nums1[p1]
                p1 -= 1
            else:
            	nums1[k] = nums2[p2]
                p2 -= 1

            k -= 1