[LeetCode] Daily LeetCode: 1827, 977

1827. Minimum Operations to Make the Array Increasing

Problem type - Greedy

🧩 Problem

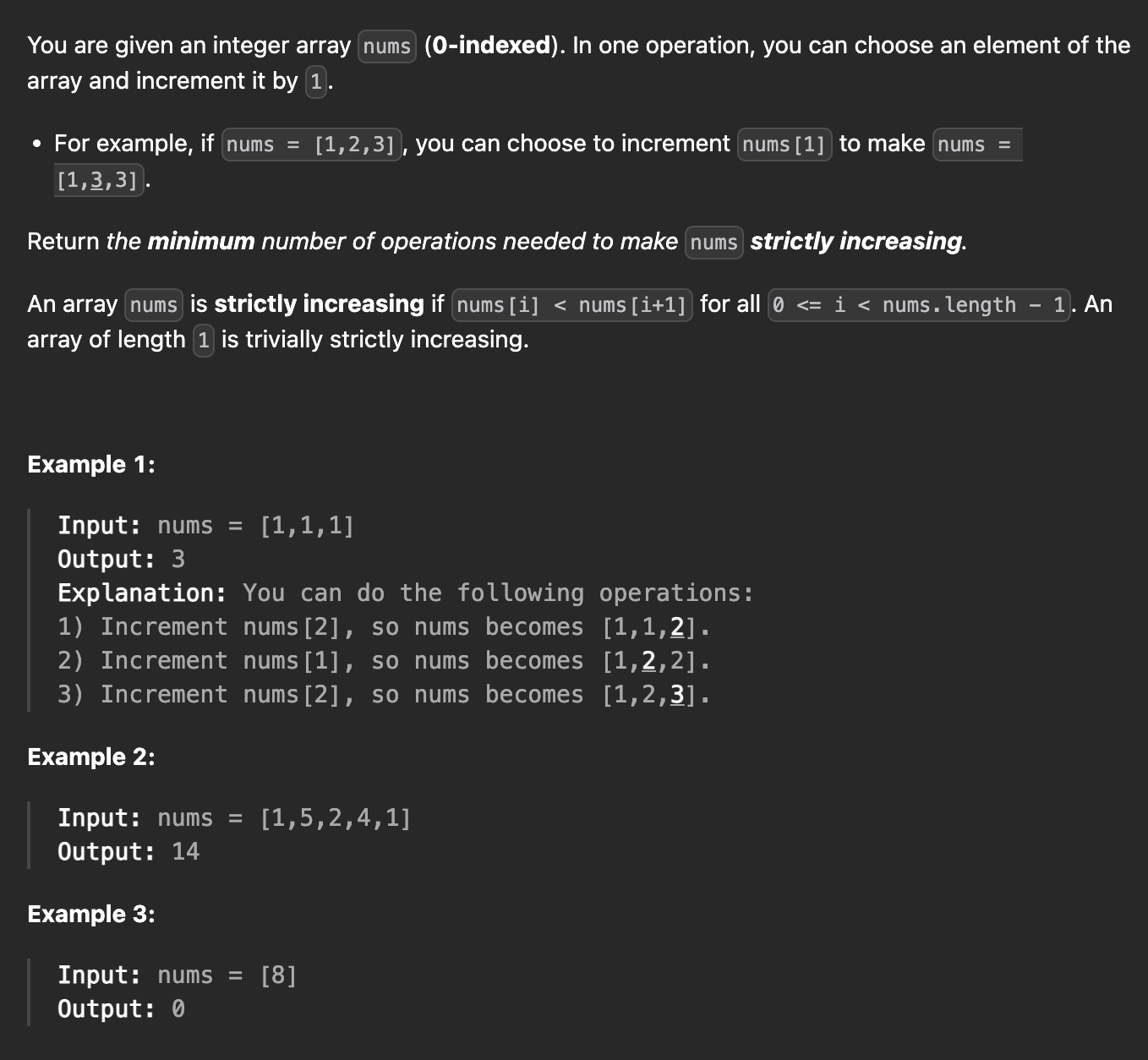
🎯 Strategy

Understand the concept

To solve this question, we need to analyze what conditions we have to derive.

The first condition is if we finish the operation, the result array(list) is strictly increasing. The second condition is to choose an element and increase the element by 1 in each operation.

Pseudocode

Now, we have two conditions given, which can start writing the pseudocode.

# Pseudocode
'''
In order to make the array increase, we have to compare two values.
Loop through the array, starting on index = 1,

for i in range(1, len(nums)):
	# if currentNum(nums[i]) smaller than previous,
    # count should be increased by the difference + 1
    # in the end, currentNum should be 1 bigger than the previous
    return result
'''

Pseudocode - 2

To elaborate on the difference between two numbers + 1, I’d use the Example 2 in the question.

When (currentNum) num[i] == 2 and (previous) num[i-1] == 5, we have to make the current number to be 6 (previous + 1).

Hence, the operation count goes up 3 => 4 => 5 => 6 because we have to increment it by 1. And we can derive the formula of previous - current + 1 == operation count

You can apply this to any circumstances in this question. Remember to add all of the operations counts together and return.

Pseudocode - 3

The final process is the implementation.

def minOperations(self, nums: List[int]) -> int:
	result = 0

    for i in range(1, len(nums)):
    	if nums[i] <= nums[i-1]:
        	result += (nums[i-1] - nums[i] + 1)
            nums[i] = nums[i-1] + 1

	return result

The time complexity is O(n), and the space complexity is O(1).

📌 Thoughts

I struggled to understand the problem’s concept and find the operation count formula.

The first thing that came up in my head was, “What is strictly increasing? Do I have to make 5 6 7 8 9 or 1 5 6 7 8?” Then, I write all the possible combinations. But it turned out I should use a more mathematical approach.

💻 Solution

Brute force approach

def minOperations(self, nums: List[int]) -> int:
	result = 0

    for i in range(1, len(nums)):
    	if nums[i] <= nums[i-1]:
        	result += (nums[i-1] - nums[i] + 1)
            nums[i] = nums[i-1] + 1

	return result

977. Squares of a Sorted Array

Problem type - Array

🧩 Problem

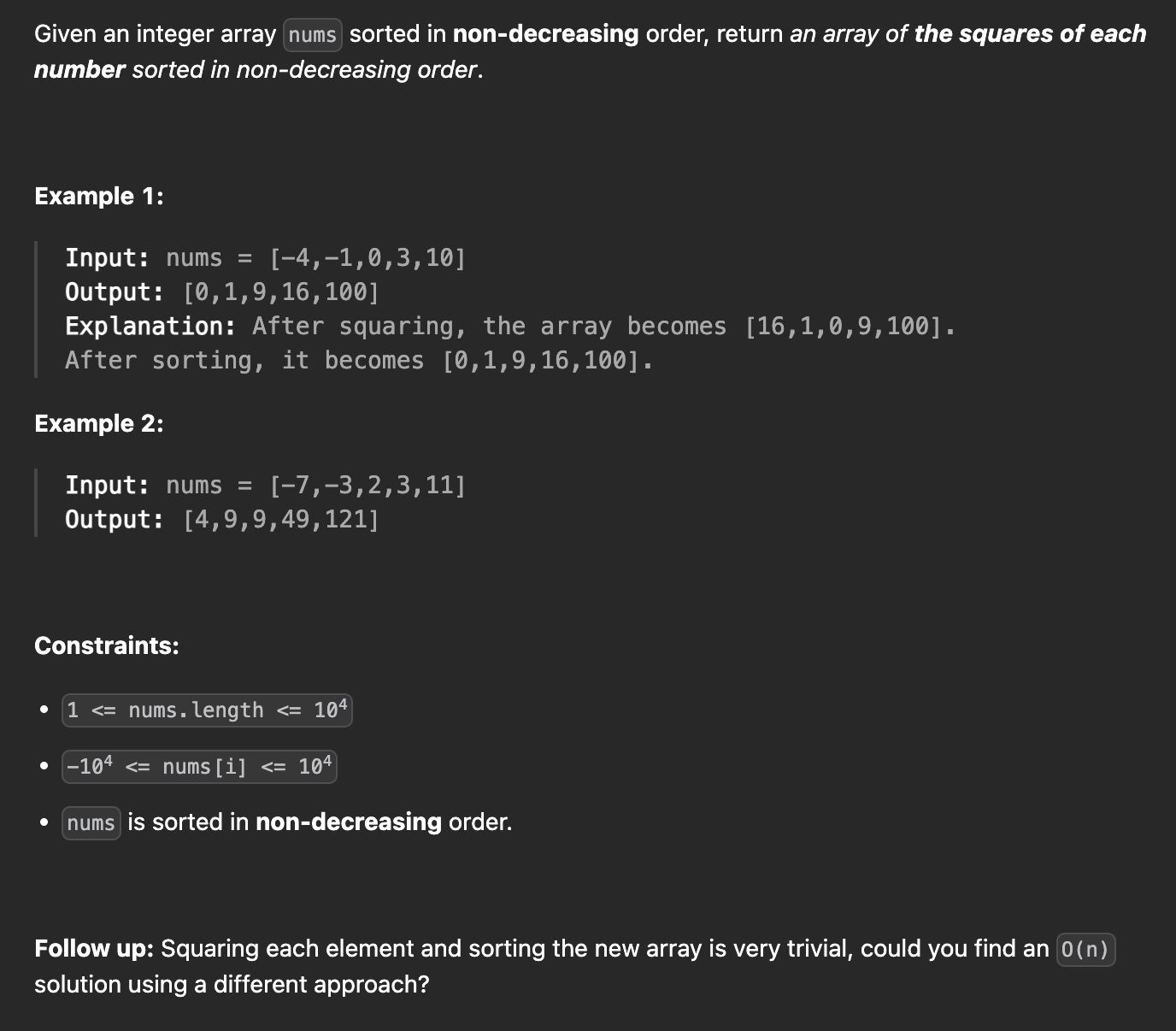
🎯 Strategy

Three approaches

Since solving this with the regular loop is considered easy for coding test questions, I practiced two more ways to solve this problem.

This post will cover basic for-loop, list comprehension, and the pointer approach.

Basic for-loop

We want to write this in for-loop for the basic understanding of this problem and list comprehension.

def sortedSquares(self, nums: List[int]) -> List[int]:
	resultList = []

    for items in nums:
    	resultList.append(items**2)

	return sorted(resultList)

Let’s condense this code into one-liner code.

List comprehension

We should use the list comprehension to make a for-loop in one line. The basic concept is the same, except it is a one-line code.

def sortedSquares(self, nums: List[int]) -> List[int]:
	return sorted([num * num for num in nums])

The time complexity is O(nlogn), and the space complexity is O(n).

Pointer approach

The last approach is the pointer approach, which can be used in coding tests, and indeed, it could be a company coding test level.

Let’s assume that we count from the left and the right of the array num.

Make the length of the nums as a variable N since it is reusable.

Set up the left = 0 and right = N - 1 as two pointers. N - 1 is the last index of the nums array.

Then, make the result array with the value of 0s that has the same length as the array nums, and we will set up another pointer, currentPoint, to update the result array, track, and set a condition for while-loop.

For the sake of memory, we are going to use the abs() function only on the left side since the examples show negative values on the left side.

def sortedSquares(self, nums: List[int]) -> List[int]:
	N = len(nums)

    left = 0
    right = N - 1

    result = [0] * N
    currentPoint = N - 1

    while currentPoint >= 0:
    	if abs(nums[left]) > nums[right]:
        	result[currentPoint] = nums[left] * nums[left]
            left += 1
        else:
        	result[currentPoint] = nums[right] * nums[right]
            right -= 1

        currentPointer -= 1

	return result

The time complexity is O(n), and the space complexity is O(n).

📌 Thoughts

I fully understood the first two approaches, but the two-pointer approach is still quite challenging.

The concept of the currentPoint was not easy to understand at first glimpse, but I spent some time trying to understand the problem. I still need a lot of practice on these topics.

💻 Solution

Brute force approach

def sortedSquares(self, nums: List[int]) -> List[int]:
	return sorted([num * num for num in nums])

Pointer approach

def sortedSquares(self, nums: List[int]) -> List[int]:
	N = len(nums)

    left = 0
    right = N - 1

    result = [0] * N
    currentPoint = N - 1

    while currentPoint >= 0:
    	if abs(nums[left]) > nums[right]:
        	result[currentPoint] = nums[left] * nums[left]
            left += 1
        else:
        	result[currentPoint] = nums[right] * nums[right]
            right -= 1

        currentPoint -= 1

    return result